城大學者頂刊發表計算物理工具探索科學計算新範式

澳門城市大學大健康學院田洋助理教授和孫沛教授擔任通訊作者的研究論文“Koopman neural operator as a mesh-free solver of non-linear partial differential equations”已在科學引文索引（SCIE）Q1頂刊、計算物理和數值計算重要期刊《Journal of Computational Physics》上發表。

R2-3-0_Article Cover (1).png

研究概述

該研究論文爲探索非線性微分方程求解以及動力系統預測的神經算子方案提供了高效、可靠的方案。本文在2024年06月13日上線後已被引用23次，開源代碼庫KoopmanLab獲得207個Star。

R2-3-1_KoopmanLab (1).png

此外，KNO已被華爲公司的機器學習框架Mindspore收錄爲流體力學和氣象科學的求解基礎工具。

R2-3-2_MindSpore 1 (1) (1).png

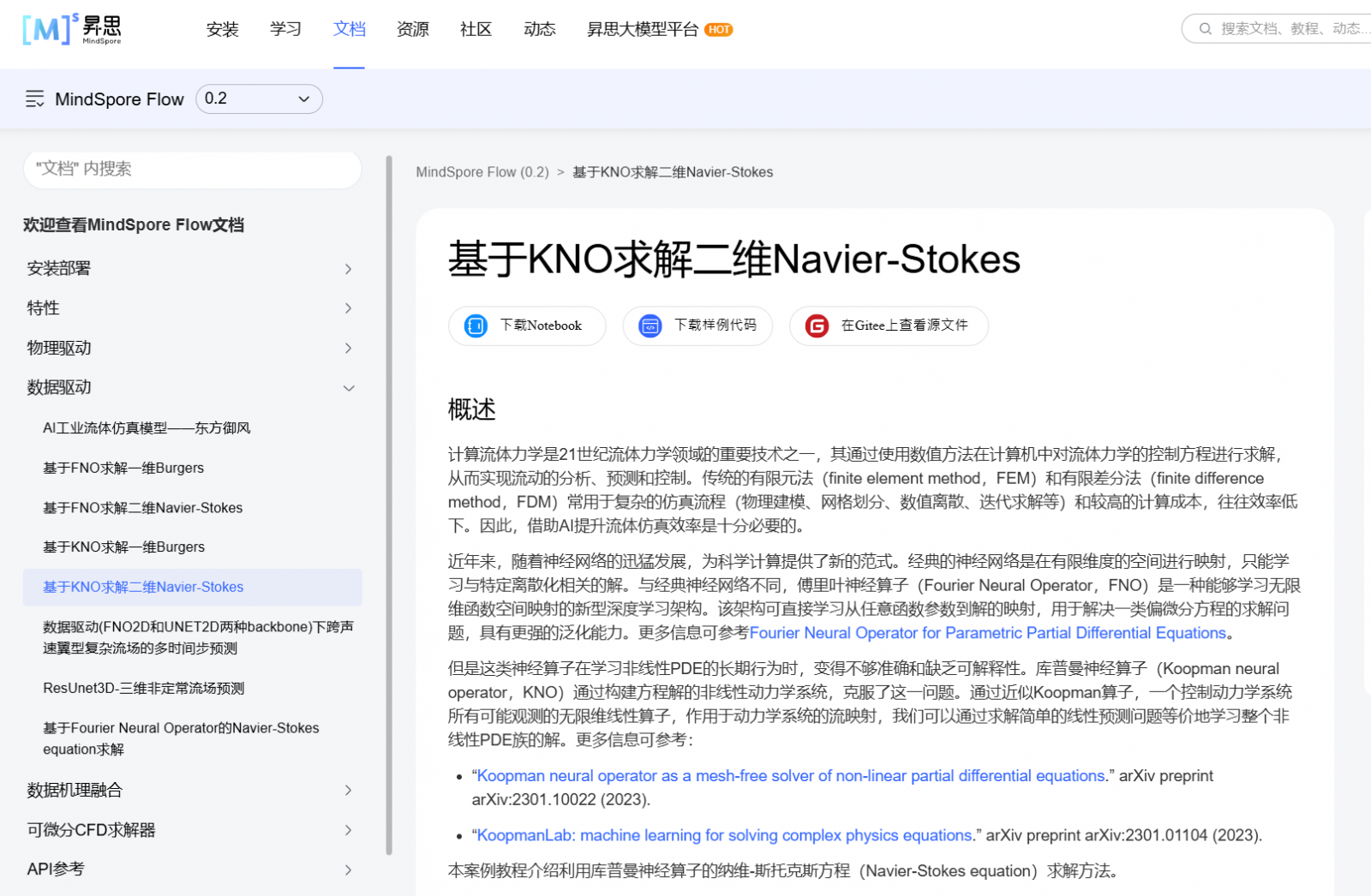
圖自Mindspore網站：Mindspore 首頁→文檔→科學計算套件→MindSpore Flow 流體仿真領域套件→數據驅動欄目

R2-3-3_MindSpore 2 (2).png

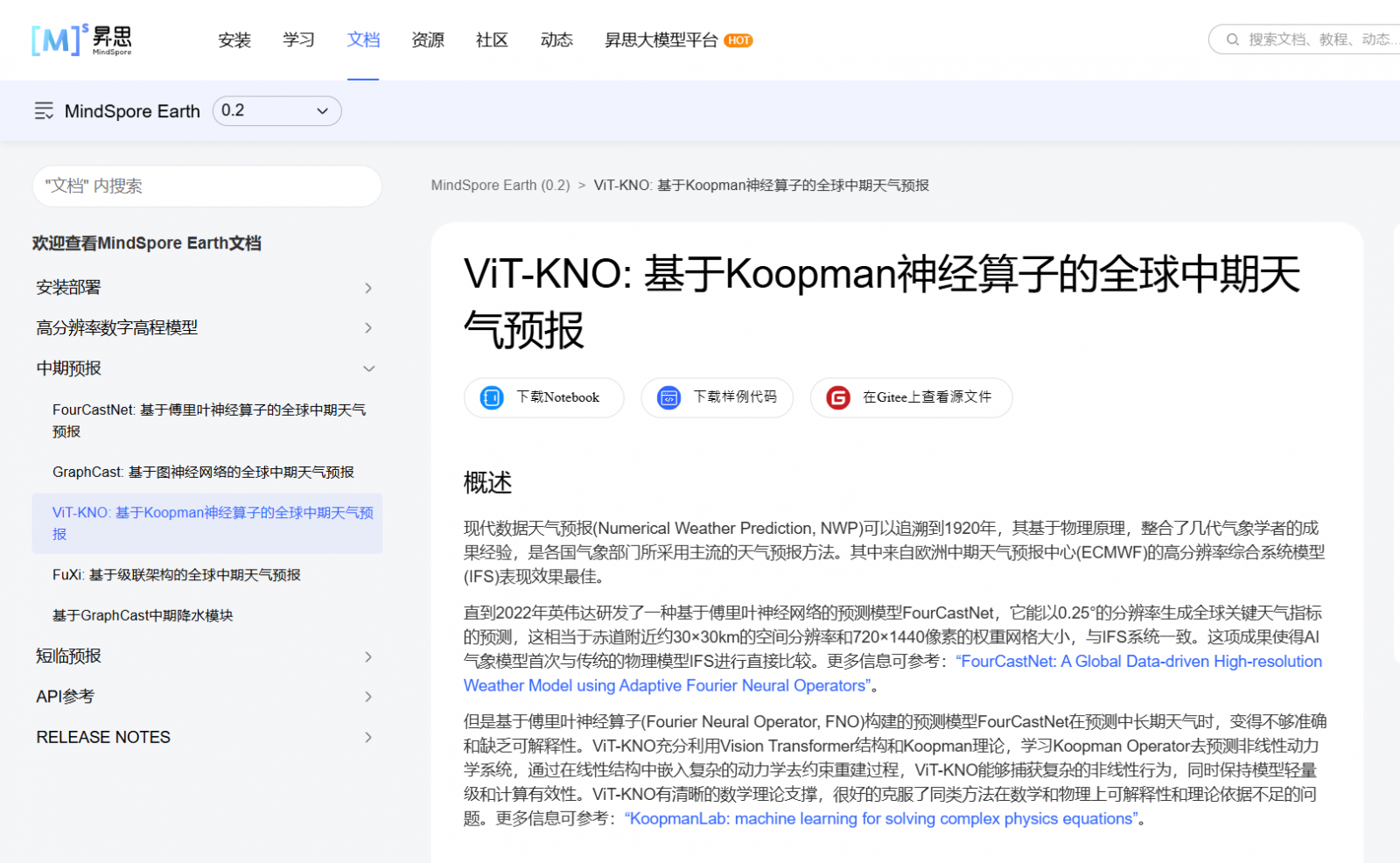
圖自Mindspore網站：Mindspore 首頁→文檔→科學計算套件→MindSpore Earth 地球科學領域套件→中期預報欄目

研究內容及發現

研究者針對現有神經算子參數化格林函數法求解微分方程的方案對非線性系統求解精度不足的問題，將動力系統理論中的Koopman算子理論引入到格林函數法迭代過程中。

R2-3-4_Unlabelled Figure.png

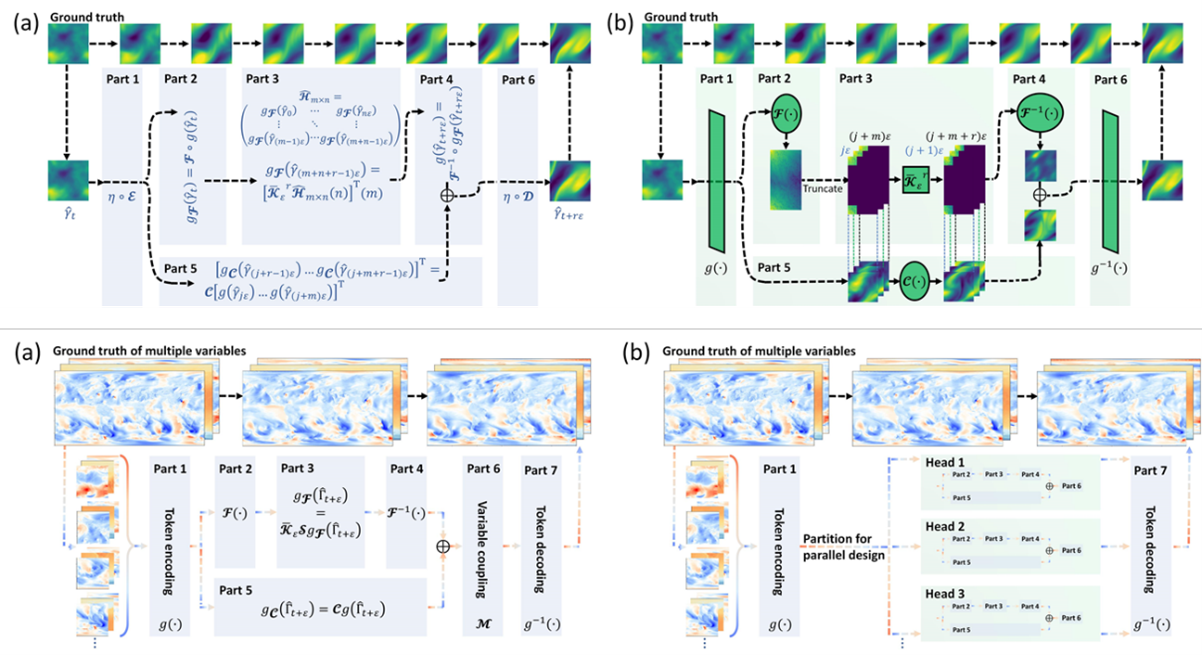
具體來說，研究者設計出了一套通用的神經網絡參數化方案，將任意微分方程或動力系統劃分爲低頻和高頻分量。高頻分量的含時演化將得到卷積變換的提取，而低頻分量的含時演化將在傅里葉空間中形成一個非線性動力系統。研究者通過定義合理的觀測函數參數化方法，將低頻分量的非線性動力系統映射至Koopman算子的不變子空間，使其在該空間中進行線性含時演化，從而能使用一個線性算法進行參數化和預測。

R2-3-5_Figure 3.jpg

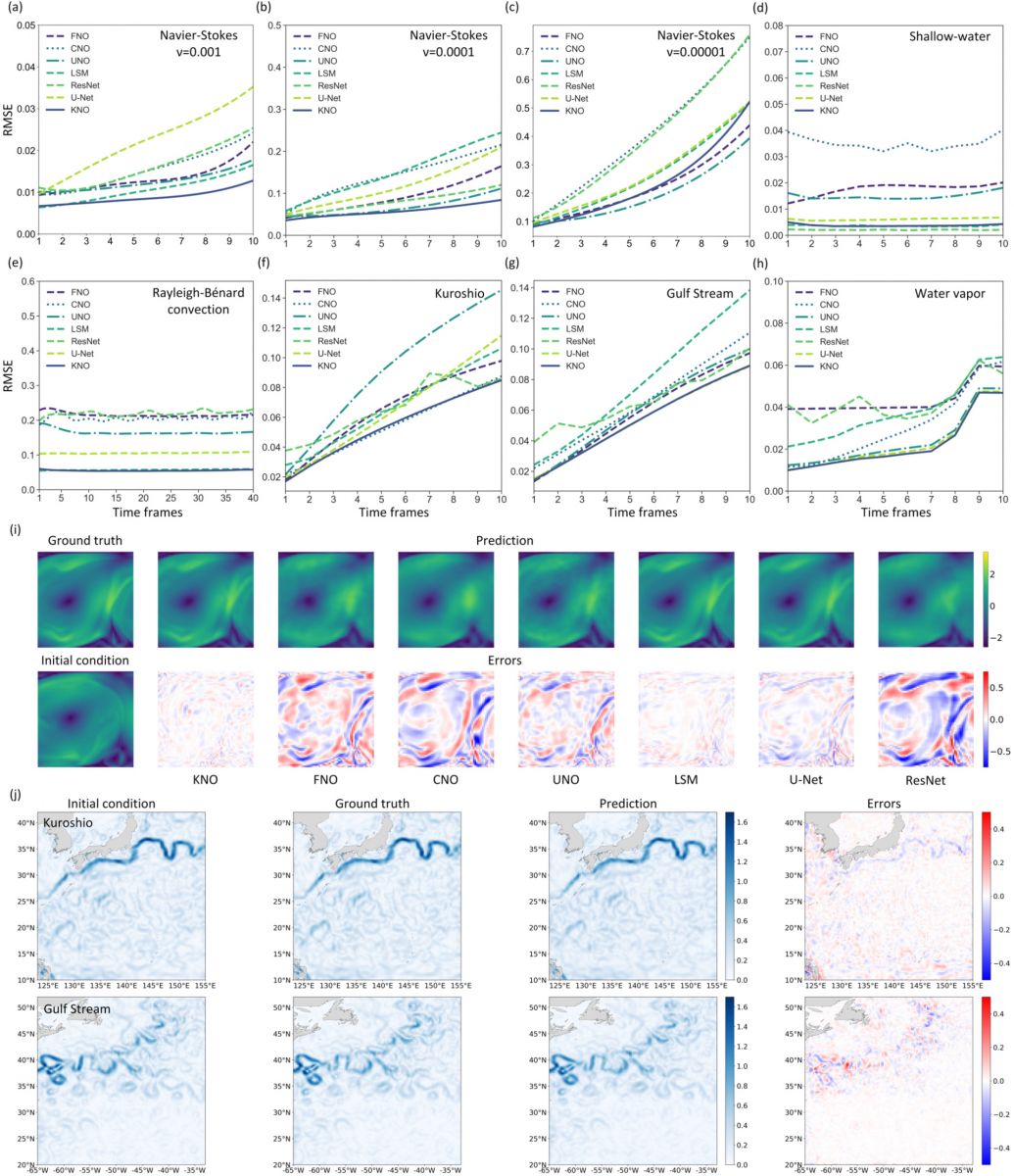
基於該框架，研究者能夠使用極小參數量的神經網絡對微分方程進行分解和計算，從而能對微分方程描述的科學計算問題進行高效數值求解。

R2-3-6_Figure 5.jpg

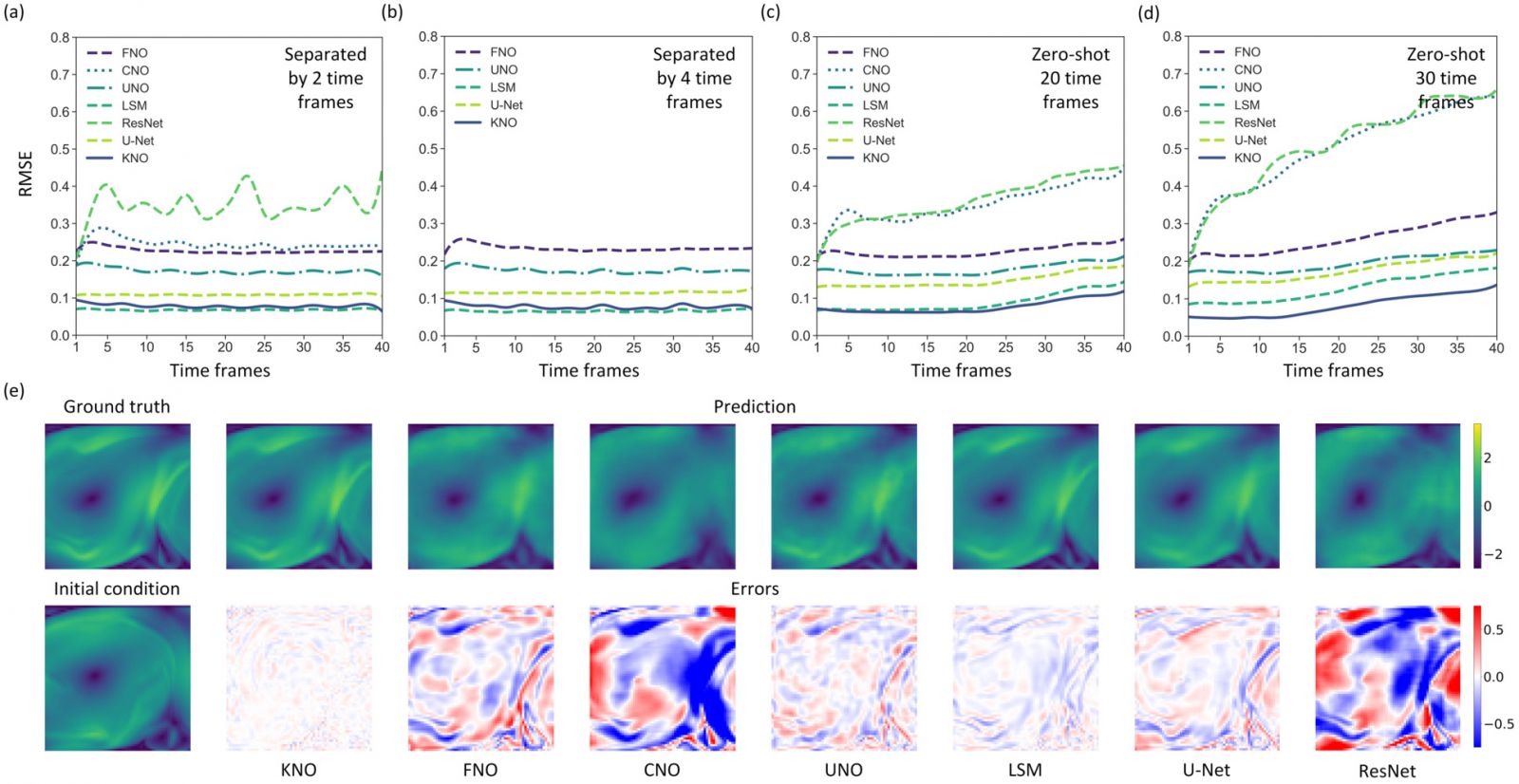
研究貢獻

在湍流模擬、流體熱學計算、全球尺度水汽分佈預測、全球西邊界流及其誘發的極端氣象預測、20個主要氣象要素在全球範圍內的長時程預測任務中，研究者提出的KNO模型不僅相較於學界常用的傅里葉神經算子（FNO）和隱式譜方法（LSM）取得了更高的求解精度和更小的模型複雜度，還相對於英偉達公司和加州理工聯合設計的FourCastNet等大型地球科學計算框架取得了更好的長程預測精度和跨條件泛化能力。

R2-3-6_Unlabelled Figure.png

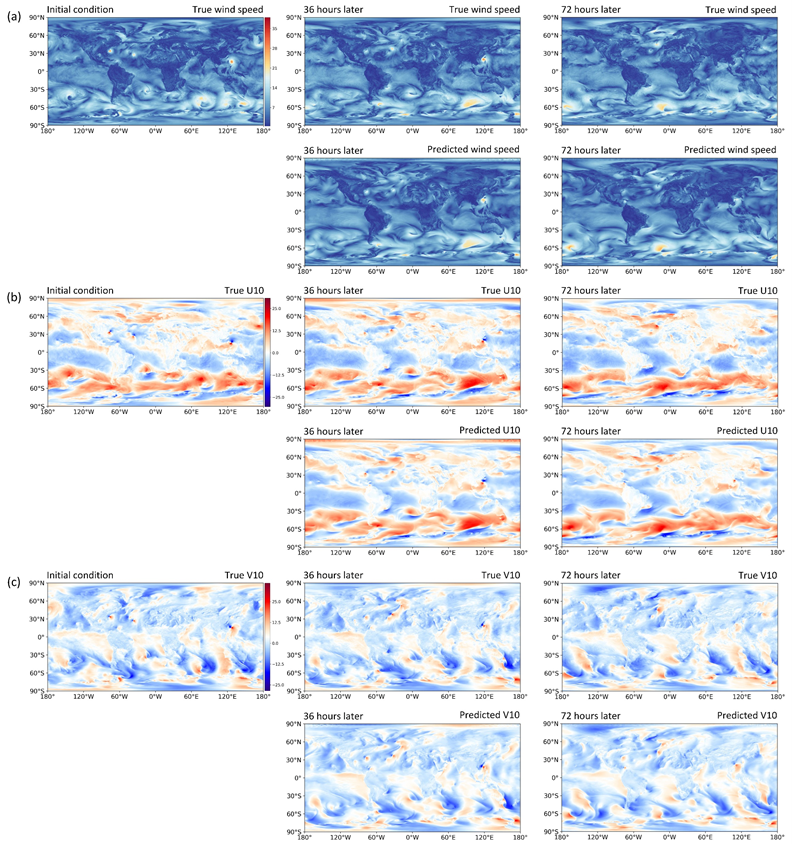
全文鏈接

本文DOI：https://doi.org/10.1016/j.jcp.2024.113194