澳門城市大學大健康學院田洋助理教授和孫沛教授擔任通訊作者的研究論文“Quasi-critical dynamics in large-scale social systems regulated by sudden events”已在科學引文索引（SCIE）Q1頂刊、數學物理和複雜系統領域重要期刊《Chaos》上發表。

研究概述

在本文中，研究者收集了長達5年的銷售數據，包括19萬餘人在2018年到2022年間的近220萬份線上消費訂單記錄。基於該數據，研究者對大規模社會系統遭遇突發事件（例如新冠疫情）時形成的準臨界動力學提供了關鍵證據。

研究內容

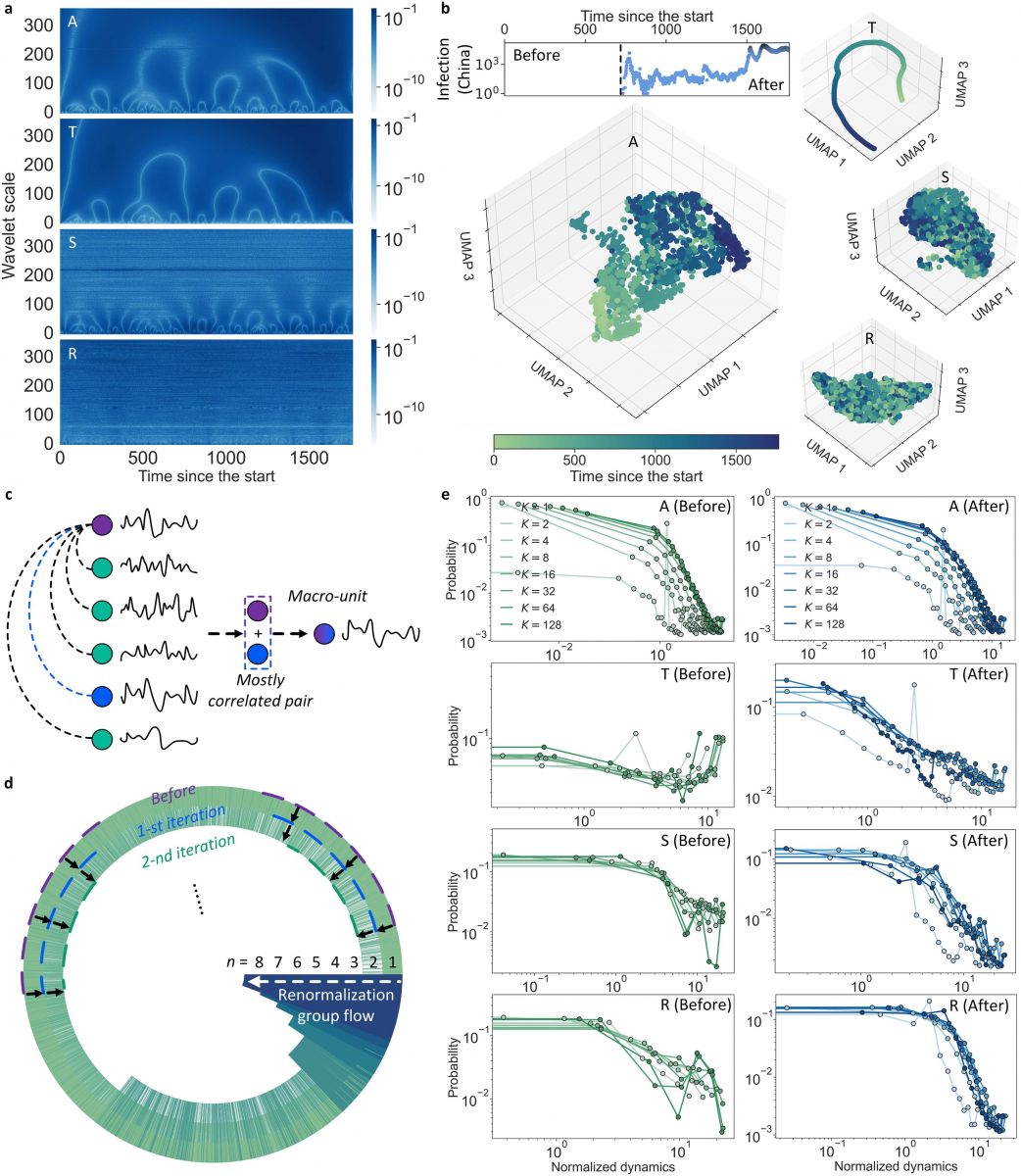
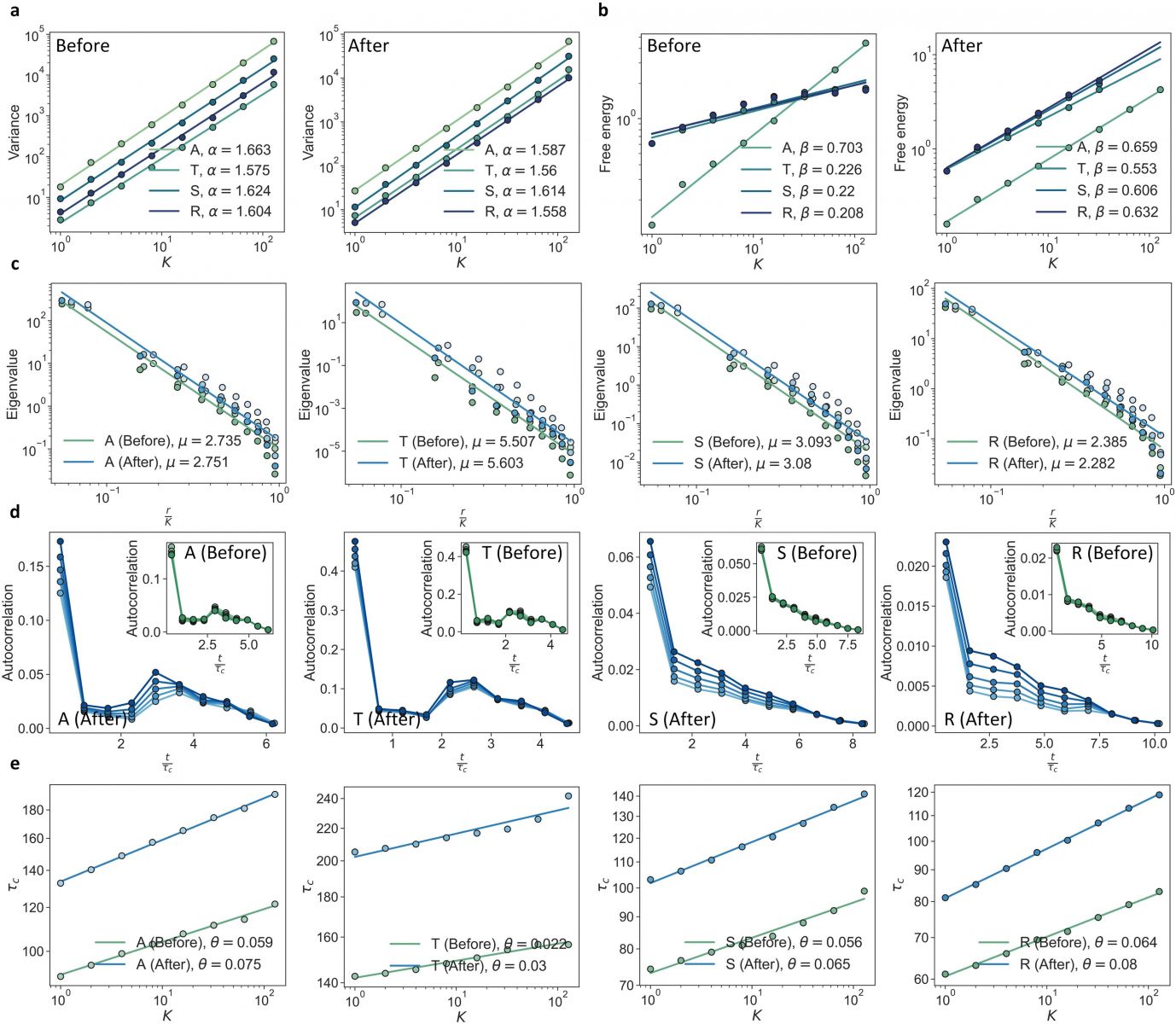
在數據分析中，研究者首先設計了一個機器學習數據處理框架，幫助對所有訂單信息進行數據清洗和歸類，從而提取了6830份常見商品在1765天中的購買頻率序列。2019年下半年，國內出現新冠疫情，對整個社會系統形成了突發干擾，這為研究者提供了分析突發事件對社會系統動力學產生影響的機會。爲了在物理層面進行定量的分析，研究者首先使用了奇異譜分析方法將社會系統的動力學分解爲趨勢、週期和隨機項。而後，研究者使用了一種唯象的重整化群分析了該社會系統的各項動力學分量在長程和短程時間尺度上的行爲。該重整化群的不穩定不動點預示着系統的動力學存在特定臨界點，對應着連續相變過程。

重要發現

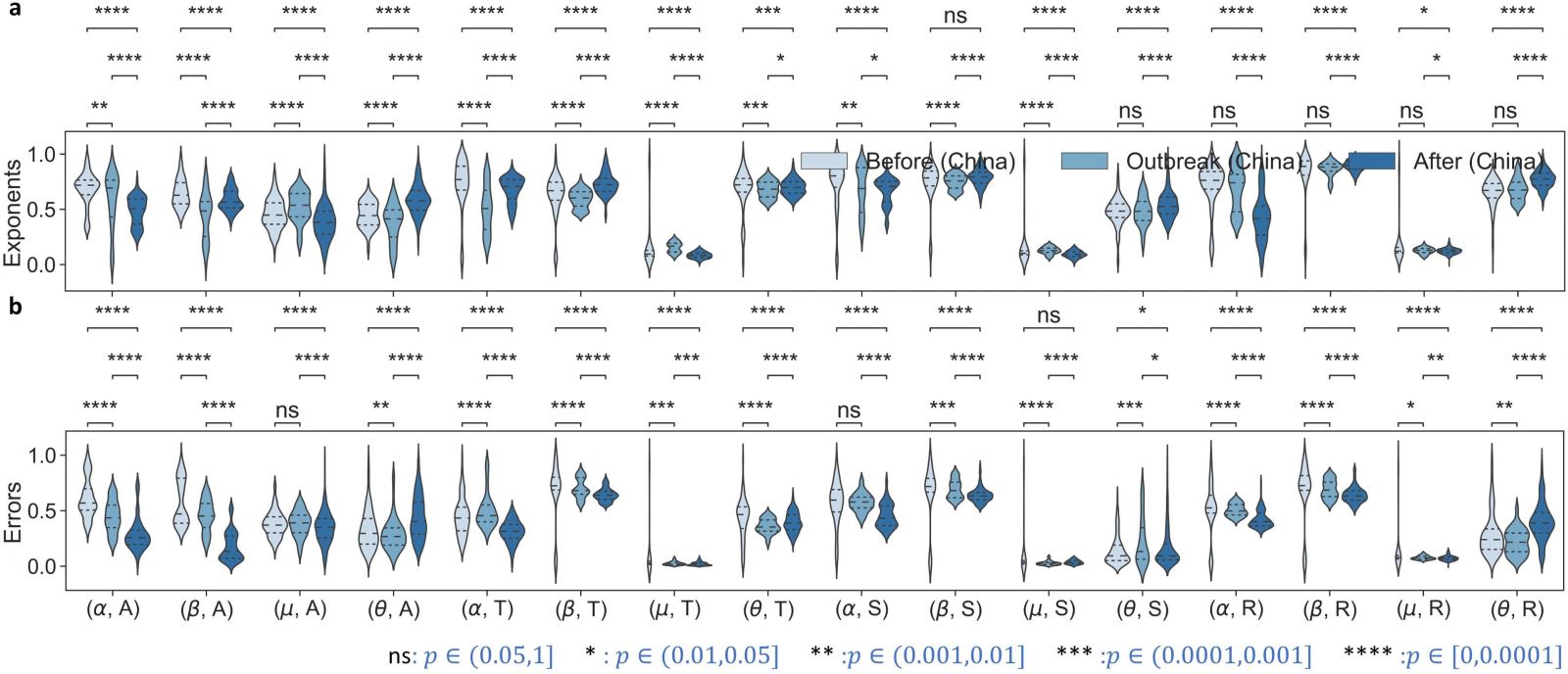
研究結果表明，在長程時間尺度，疫情的爆發使得社會系統的所有動力學分量都趨向於一個特定的臨界點，從而最大化系統對突發事件的反應性（Reactivity）；在短時間尺度，社會系統的趨勢、隨機動力學分量都趨向於臨界點，而週期性分量依然保持自身的特定動力學特性，從而保持了系統自身的穩定性（Stability）。短時間尺度的特性印證了社會系統總趨於在反應性和穩定性間尋求一個動態平衡的特點。

研究貢獻

該研究從統計物理的視角入手，爲社會物理學（Social Physics）中的相關猜想提供了現實定量證據。

全文鏈接

本文DOI：https://doi.org/10.1063/5.0218422